Faktencheck Vergabemathematik: Der Logarithmus, wo keiner mit muss

Seit dem gestrigen 1. April rätselt die Vergabecommunity, ob sie im Beitrag „Faktencheck Vergabemathematik: Die natürliche Logarithmusformel“ (s. Vergabeblog.de vom 01/04/2024, Nr. 56083) gefoppt wurde. Die Antwort wird Sie überraschen.

 

Was stimmt, und was stimmt nicht?

Es stimmt fast alles – mit einer einzigen Ausnahme: Der verlinkte Aufsatz „Logarithm Induced Reduction of Price Asymmetries“ ist reinste Quatschmathematik (siehe MathGen). Nicht ein Satz in dem Aufsatz macht mathematischen Sinn. Der Aufsatztitel enthielt aber bereits einen kleinen Hinweis.

Alle anderen Aussagen im gestrigen Artikel sind aber zutreffend und faktisch richtig. Und zwar ohne jede Ausnahme.

Im Endeffekt können Sie also die natürliche Logarithmusformel als Zuschlagsformel verwenden, und es werden sinnvolle Ergebnisse herauskommen. Denn die natürliche Logarithmusformel ist nichts anderes als eine verwirrende Verbrämung der guten alten Einfachen Richtwertmethode. Es ist also völlig egal, ob Sie als Zuschlagsformel das (echte) Preis-Leistungsverhältnis Z = L/P verwenden, oder dieses Formelmonster von gestern:

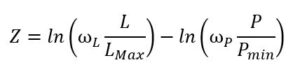
Die Auflösung

Um das zu verstehen, muss man sich nur an zwei einfache Logarithmusgesetze (siehe www.mathebibel.de) erinnern:

1) Die Produktregel: ln(a ⋅ b) = ln(a) + ln(b)

2) Die Quotientenregel: ln(a / b) = ln(a) – ln(b)

Und wenn man diese beiden Gesetze auf die obige Zuschlagsformel anwendet, dann ergibt sich eine viel einfachere Form, nämlich:

 

bzw.

Lassen Sie uns die letzte Gleichung als „Gleichung 1“ bezeichnen.

Die Gewichtungen  sind ja konstante Zahlen, zum Beispiel Prozentangaben wie 40 % zu 60 % oder 70 % zu 30 %. Wenn man den Logarithmus einer konstanten Zahl berechnet, dann ist das natürlich auch eine Konstante. Beispielsweise ist ln(40%) = -0,91629…  Dass der Wert negativ ist, spielt hier überhaupt keine Rolle.

Wenn man bei der Berechnung der Zuschlagskennzahlen bei allen Angeboten am Ende noch eine konstante Zahl dazu addiert oder subtrahiert, dann ändert sich dadurch die Rangfolge der Angebote natürlich nicht. Dazu ein Beispiel:

Angebot	A1	A2	A3
Zuschlagskennzahl Z	45,7	32,0	65,1
Zuschlagskennzahl Z + 1	46,7	33,0	66,1
Rang:	2	3	1

Dasselbe gilt natürlich, wenn man bei der Zuschlagskennzahl bei allen Angeboten dieselbe konstante Zahl abzieht.

Wenn das aber so ist, dann können wir in Gleichung 1 die Werte „ln(ω_L)“ und „ln(ω_p)“ einfach weglassen, denn das sind ja konstante Zahlen. Die Rangfolge der Angebote ändert sich dadurch nicht.

Aber momentmal: L_Max (zum Beispiel: 10.000 Punkte bei der UfAB-Wertung) und somit auch ln(L_Max) sind ja auch konstante Zahlen! Dann können wir das ja ebenfalls weglassen.

Und selbst P_min bzw. ln(P_min) sind bei der Angebotsauswertung konstante Zahlen, nämlich der niedrigste Preis aller wertungsfähigen Angebote. Zwar sind P_min bzw. ln(P_min) vor Angebotsöffnung/Submissionstermin noch nicht bekannt, aber der Wert ist trotzdem eine einheitliche, konstante Zahl für sämtliche Angebotsauswertungen.

Einzig L und P sind damit variable Werte der verschiedenen Angebote für die Berechnung von Z.

Wenn man also alle konstanten Werte aus der Gleichung 1 entfernt, dann verbleibt die neue Zuschlagsformel:

Wenn man dann die Quotientenregel „rückwärts“ anwendet, dann erhält man:

Nanu, das sieht ja schon fast wie die Einfache Richtwertmethode aus, nur dass diese noch logarithmiert ist.

Und jetzt kommen wir zu einer tollen Eigenschaft des Logarithmus: Die Logarithmusfunktion ist nämlich echt monoton steigend (wie der Mathematiker sagt).

Was bedeutet das? Das bedeutet, dass der Logarithmus einer größeren Zahl b immer (echt) größer ist als der Logarithmus einer kleineren Zahl a. Mathematisch:

b > a  ⇒  ln(b) > ln(a)

Der Logarithmus geht also immer aufwärts:

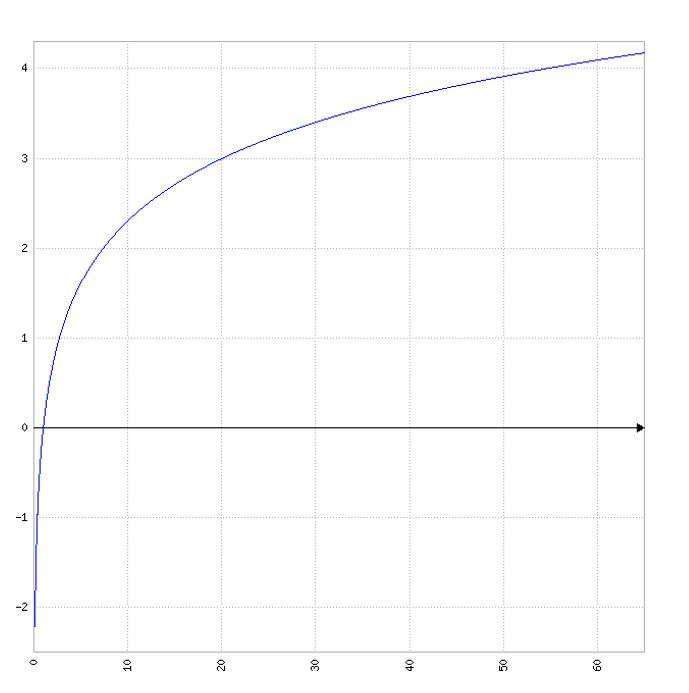
Abb.: Graph zur Funktion des natürlichen Logarithmus y = ln(x)

Wenn man also die Logarithmusfunktion auf die Zuschlagskennzahlen Z von mehreren Angeboten anwendet, dann ändert sich dadurch die Rangfolge der Angebote nicht.

Beispiel:

Angebot	A1	A2	A3
Zuschlagskennzahl Z	45,7	32,0	65,1
Logarithmus von Z = ln(Z)	3,8	3,5	4,2
Rang:	2	3	1

Fazit

Die Einfache Richtwertmethode Z = L/P und die natürliche Logarithmusformel führen zwangsläufig immer zum identischen Wertungsergebnis, nämlich dem (echten) Preis-Leistungsverhältnis.

Juristische Bedenken

Schon bei der Placeboformel (s. Vergabeblog.de vom 14/03/2024, Nr. 56066) haben viele Vergaberechtsjuristen sehr ernsthafte Bedenken, ob diese Formel zulässig wäre. Und dies trotz der Entscheidung des BGH, Beschluss vom 04.04.2017 – X ZB 3/17:

„Die Wahl einer bestimmten Preisumrechnungsmethode kann vergaberechtlich nur beanstandet werden, wenn sich gerade ihre Heranziehung im Einzelfall aufgrund besonderer Umstände als mit dem gesetzlichen Leitbild des Vergabewettbewerbs unvereinbar erweist.“

Die Argumentation lautet aus Vergaberechtssicht so, dass die Angabe von Gewichtungen, die letztlich aber keine sind, mit dem gesetzlichen Leitbild des Vergabewettbewerbs nicht vereinbar wäre.  Um solche wirkungslosen Gewichtungen handelt es sich aber ganz offensichtlich sowohl bei der Placeboformel als auch bei der Logarithmusformel.

Für die Angabe von Gewichtungen in Formeln, die aber ganz offensichtlich nicht richtig sein können (die also definitiv falsch sind) – wie bei der UfAB-II Formel oder der Interpolationsmethode –, muss dann aber dieselbe Argumentation gelten. Denn die Angabe falscher Werte muss doch schlimmer sanktioniert werden als die Angabe wirkungsloser Werte, oder?

Praxistipp

Verwenden Sie nur solche Zuschlagsformeln, die Sie vollständig verstehen. Verwenden Sie keine Zuschlagsformeln, die den Bietern falsche Gewichtungen zwischen Leistung und Preis suggerieren. Verwenden Sie insbesondere auf keinen Fall die UfAB-II Formel oder die Interpolationsmethode, weil diese Formeln falsche Gewichtungen vorspiegeln und zu erratischen und sich widersprechenden Zuschlagsergebnissen führen können, so dass völlig unklar ist, welche Gewichtungen diese Formeln tatsächlich umsetzen. Jedenfalls nicht die im jeweiligen Text angegebenen Gewichtungen!