Der Fisch an der Angel – oder: der Decoy-Effekt – lassen Sie sich (nicht) täuschen! (Teil 2 von 4)

Im ersten Teil (Vergabeblog.de vom 23/01/2020, Nr. 43117) haben wir gesehen, wie leicht Kaufentscheidungen durch Köderangebote beeinflusst werden können. Aber gilt das auch für Zuschlagsformeln, die Beschaffer bei öffentlichen Vergaben anwenden? In diesem und dem folgenden Beitrag (Teil 3) wird anhand von zwei der gebräuchlichsten Zuschlagsformeln untersucht, ob diese für den sogenannten Decoy-Effekt anfällig sind.

Die Familie der UFAB-II Formeln

Zu den (gerade auch international) weitest verbreiteten Zuschlagsformeln gehören diejenigen Formeln, die aus den Wertungspreisen Preispunkte berechnen. Dies erfolgt, indem der einzelne Wertungspreis eines Angebots in das reziproke Verhältnis zum billigsten Wertungspreis der wertungsfähigen Angebote gesetzt wird. Diese Formeln haben also stets die Grundform:

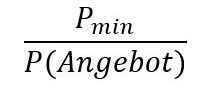
Diese Formeln können immer leicht daran erkannt werden, dass der Wertungspreis P(Angebot) im Nenner steht.

Das billigste Angebot erhält damit den Wert P_min/P_min = 1 und alle andere (teureren) Angebote einen Wert zwischen 0 und kleiner 1. Wenn beispielsweise der niedrigste (Preis P_min) aller Angebote 300 Euro beträgt, dann erhält ein Angebot mit dem Wertungspreis 400 Euro den Wert 0,75 (300 Euro / 400 Euro).

Es gibt einen ganzen Strauß verschiedener Ausprägungen dieser Zuschlagsformeln. Sie sind immer dadurch gekennzeichnet, dass der Wertungspreis des einzelnen Angebots im Nenner steht. Da diese Formelvariationen letztlich alle dieselben Schwächen aufweisen, nennt der Autor dieses Artikels die Gesamtheit aller dieser Formeln vereinfachend die (Familie der) UfAB-II-Formel(n), da bereits im Jahr 1988 eine solche Ausprägung in der damals erschienenen UfAB-II veröffentlicht wurde (jedoch im Jahr 2003 mit der UfAB III bereits wieder kassiert wurde).

Der Decoy-Effekt und die UFAB-II Formel

Für unsere hiesige Untersuchung wählen wir folgenden Vertreter der UfAB-II Formeln:

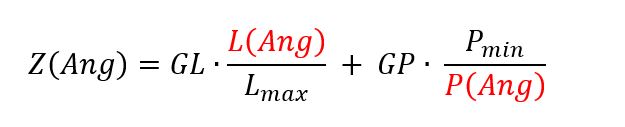
Z(Ang) ist dabei die berechnete Zuschlagskennzahl für ein Angebot mit der Leistungswertung L(Ang) und dem Wertungspreis P(Ang).
GL und GP sind die beabsichtigten Gewichtungen für die Leistung bzw. den Preis. L_max ist die maximal erreichbare Leistungspunktzahl.
Das Angebot, das die höchste Zuschlagskennzahl erreicht, erhält den Zuschlag.

Zahlenbeispiel:

Angenommen,

– die Leistungswertung eines Angebots sei L(Ang) = 30,

– die maximal erreichbare Leistungswertung sei L_max = 64.

– der Wertungspreis des Angebots sei P(Ang) = 400 Euro,

– der niedrigste Preis aller Angebot sei P_min = 300 Euro,

– die Gewichtung der Leistung sei GL = 60 % und die Gewichtung des Preises sei GP = 40%

Dann ergibt sich als Zuschlagskennzahl für dieses Angebot:

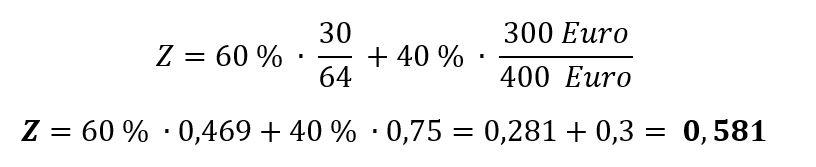
Diese UfAB-II Formel soll nun auf die beiden in Teil 1 (Vergabeblog.de vom 23/01/2020, Nr. 43117) angegebenen beispielhaften Dreierkonstellationen (Wikipedia-Beispiel) angewendet werden, um jeweils das Gewinnerangebot zu ermitteln.

Dazu muss das Wikipedia-Beispiel noch um eine Gewichtung zwischen Leistung und Preis ergänzt werden. Da uns die Leistung (Speicherplatz) wichtig ist, entscheiden wir uns für eine Gewichtung der Leistung von 60 % und eine Gewichtung des Preises von 40 %. Als L_max nehmen wir für das Beispiel 64 GB, da es sich bei den Produkten um MP3-Player der Mittelklasse handelt. Der Einfachheit halber nehmen wir als Leistungspunkte das Gigabyte-Speichervolumen des Produkts. Beispielsweise ergeben 64 GB Speicherplatz dann also 64 Leistungspunkte.

Nun haben wir alle Parameter beisammen und können in den beiden Konstellationen jeweils die Zuschlagskennzahlen für die Angebote A, B, C1 und C2 berechnen, wobei wir für das Köderangebot C2 abweichend vom Wikipedia-Beispiel in Teil 1 nicht 350 Euro, sondern 265 Euro ansetzen:

Beispiel mit Köderangebot C1:

GL = 60 %; GP= 40 %; L_max = 64 GB; P_min = 300 € (nämlich der Wertungspreis von B)

Angebot	Ang. A	Ang. B	Ang. C1
Leistung L(Ang)	30 GB	20 GB	25 GB
Preis P(Ang)	400 €	300 €	450 €
Z(Ang) =	0,581	0,588	0,501

Die Zuschlagskennzahl für Angebot A hatten wir schon ausgerechnet, denn im obigen Zahlenbeispiel haben wir genau die Angebotswerte von Angebot A verwendet. Die Zuschlagskennzahlen der Angebote B und C1 berechnen sich entsprechend.

Da das Angebot B die höchste Zuschlagskennzahl hat, gewinnt also dieses Angebot B.

Beispiel mit Köderangebot C2 statt C1:

GL = 60 %; GP= 40 %; L_max = 64 GB; P_min = 265 € (nämlich jetzt der Wertungspreis von C2)

Angebot	Ang. A	Ang. B	Ang. C2
Leistung L(Ang)	30 GB	20 GB	15 GB
Preis P(Ang)	400 €	300 €	265 €
Z(Ang) =	0,546	0,541	0,541

Jetzt gewinnt Angebot A! Da das Angebot C2 einen anderen Preis als das Angebot B ausweist, verändert sich in der Formel der Wert P_min, und alle Angebote erhalten neue Zuschlagskennzahlen.

Das Ergebnis überrascht!

Zunächst liegen sämtliche Zuschlagskennzahlen relativ nahe beisammen. Also war das Endergebnis auch mit einer mathematischen Auswertung (statt dem in Teil 1 erwähnten Bauchgefühl) knapp.

Im Szenario mit dem Köderangebot C1 hat das Angebot B die höchste Zuschlagskennzahl erreicht und erhält den Zuschlag.

Im Szenario mit dem Köderangebot C2 hat das Angebot A die höchste Zuschlagskennzahl erreicht und erhält den Zuschlag.

Die Angebotswerte der Angebote A und B wurden aber nicht verändert.

Das heißt, nur die Einführung eines Köderangebots bzw. die Änderung der Merkmale des Köderangebots hat – trotz scheinbar unbestechlicher Zuschlagsformel – die Zuschlagsentscheidung beeinflusst!

Fazit

Es lässt sich mithin festhalten, dass durch die Verwendung dieser UfAB-II Formel der Decoy-Effekt im Vergabewesen institutionalisiert wird. Man könnte denken, durch die Anwendung einer unbestechlichen und scheinbar neutralen Zuschlagsformel befreie man sich von solchen Täuschungseffekten; aber genau das Gegenteil ist richtig. Schlimmer noch, die unterstellte Unbestechlichkeit und Neutralität verschleiert erst recht die Anfälligkeit dieser Formel für den Decoy-Effekt.

Und noch etwas fällt auf (was wir hier aber nicht weiter vertiefen wollen): Im ersten Teil (Vergabeblog.de vom 23/01/2020, Nr. 43117) dieser Artikelserie wurde bereits beschrieben, dass das Köderangebot C1 so gewählt ist, um den Absatz von Produkt A zu fördern, also das Angebot A attraktiver aussehen zu lassen. Die UfAB-II-Formel entscheidet sich jedoch für das Angebot B und konterkariert damit die beabsichtigte Wirkung von C1!

Aber kann es noch schlimmer kommen? Wenn Sie starke Nerven haben, dann freuen Sie sich auf Teil 3 dieser Artikelserie.

Anmerkung der Redaktion

Teil 1: „Ein Beispiel für den Decoy-Effekt“ erschien im Vergabeblog.de vom 23/01/2020, Nr. 43117.
Teil 3: Der Decoy-Effekt und die Interpolationsformel erschien auf Vergabeblog.de vom 06/02/2020, Nr. 43129
Teil 4: Mathematische Würdigung und Praxistipp auf Vergabeblog.de vom 13/02/2020, Nr. 43133.