 Wir haben gelernt, dass mit Köderangeboten Kaufentscheidungen beeinflusst werden können. Und zwar nicht nur auf verkaufspsychologischer Ebene bei Menschen (siehe Teil 1, ), sondern zumindest auch eine Variante der international sehr verbreiteten UfAB-II Formeln (siehe Teil 2, ). Neben der UfAB-II Formel wird in Deutschland außerdem vor allem eine Variante der Interpolationsformeln sehr stark genutzt, weil sie in vielen Vergabehandbüchern (z.B. Vergabehandbuch des Bundes) vorgegeben ist.
Wir haben gelernt, dass mit Köderangeboten Kaufentscheidungen beeinflusst werden können. Und zwar nicht nur auf verkaufspsychologischer Ebene bei Menschen (siehe Teil 1, ), sondern zumindest auch eine Variante der international sehr verbreiteten UfAB-II Formeln (siehe Teil 2, ). Neben der UfAB-II Formel wird in Deutschland außerdem vor allem eine Variante der Interpolationsformeln sehr stark genutzt, weil sie in vielen Vergabehandbüchern (z.B. Vergabehandbuch des Bundes) vorgegeben ist.
Die häufigst genutzte Interpolationsformel
Aus der Familie der Interpolationsformeln wählen wir also für unsere Untersuchung folgende Ausprägung als der gerade in Deutschland meistgenutzten Variante. Hier werden die Preispunkte folgendermaßen ermittelt:
Das Angebot mit dem niedrigsten Preis erhält die maximalen Preispunkte; ein Angebot mit einem fiktiv doppelt so hohen Preis (und alle noch teureren Angebote) erhalten null Preispunkte. Für die restlichen preislich dazwischen liegenden Wertungspreise werden die Preispunkte mittels linearer Interpolation berechnet. Hieraus ergibt sich folgende Gesamtformel für die Zuschlagskennzahl Z im Interpolationsbereich (wenn Pmin ≤ P(Ang) ≤ 2⋅ Pmin ist):
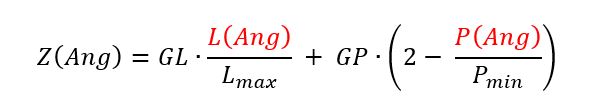
Der Decoy-Effekt und die Interpolations-Formel
Für unsere Untersuchung wählen wir diesmal eine Gewichtung von 70 % für die Leistung und 30 % für den Preis, da die Interpolationsformeln erfahrungsgemäß im Vergleich zu anderen Zuschlagsformeln extrem preissensitiv sind. Sämtliche anderen Werte bleiben identisch zum Beispiel für die UfAB-II Formel aus Teil 2 (), also sowohl die Angebotswerte als auch die maximale Leistungspunktzahl Lmax = 64 GB.
Damit ergibt sich unter Anwendung dieser Formel rechnerisch folgendes Ergebnis:
Beispiel mit Köderangebot C1:
GL = 70 %; GP= 30 %; Lmax = 64 GB; Pmin = 300 € (nämlich der Wertungspreis von B)
| Angebot | Ang. A | Ang. B | Ang. C1 |
| Leistung L(Ang) | 30 GB | 20 GB | 25 GB |
| Preis P(Ang) | 400 € | 300 € | 450 € |
| Z(Ang) = | 0,528 | 0,519 | 0,423 |
Rechenbeispiel für Angebot A:
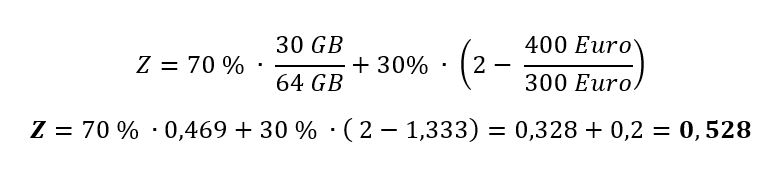
Die Zuschlagskennzahlen der Angebote B und C1 berechnen sich entsprechend. Da das Angebot A die höchste Zuschlagskennzahl hat, gewinnt hier also Angebot A.
Beispiel mit Köderangebot C2:
GL = 70 %; GP= 30 %; Lmax = 64 GB; Pmin = 265 € (nämlich jetzt der Wertungspreis von C2)
| Angebot | Ang. A | Ang. B | Ang. C2 |
| Leistung L(Ang) | 30 GB | 20 GB | 15 GB |
| Preis P(Ang) | 400 € | 300 € | 265 € |
| Z(Ang) = | 0,475 | 0,479 | 0,464 |
Jetzt gewinnt Angebot B! Da das Angebot C2 einen anderen Preis als das Angebot B ausweist, verändert sich in der Formel der Wert Pmin, und alle Angebote erhalten neue Zuschlagskennzahlen.
Im Szenario mit dem Köderangebot C1 hat das Angebot A die höchste Zuschlagskennzahl erreicht und erhält den Zuschlag.
Im Szenario mit dem Köderangebot C2 hat das Angebot B die höchste Zuschlagskennzahl erreicht und erhält den Zuschlag.
Die Angebotswerte der Angebote A und B wurden aber nicht verändert.
Das heißt, nur die Einführung eines Köderangebots bzw. die Änderung der Merkmale des Köderangebots hat – trotz scheinbar unbestechlicher Zuschlagsformel – die Zuschlagsentscheidung beeinflusst!
Fazit
Und da haben wir das Malheur! Auch diese meistgebräuchliche Interpolationsformel ist anfällig für den Decoy-Effekt, denn je nach Wahl des Köderangebots C1 oder C2 gewinnt entweder das Angebot A oder das Angebot B.
Und jetzt? „que fair?“ – Was kann ich – was muss ich tun? Wie kann ich mich als Beschaffer vor dem Decoy-Effekt schützen?
Seien Sie gespannt auf den abschließenden Teil 4 dieser kleinen Artikelserie.
Anmerkung der Redaktion
Teil 1: Ein Beispiel für den Decoy-Effekt erschien auf Vergabeblog.de vom 23/01/2020, Nr. 43117
Teil 2: Der Decoy-Effekt und die UfAB-II Formel auf
Teil 4: Mathematische Würdigung und Praxistipp auf .
Wolfgang Bartsch
Dipl.-Inform. (univ.) Wolfgang Bartsch ist Managing Consultant im Bereich Beschaffungsberatung bei der IABG mbH. Er berät öffentliche Auftraggeber und Bieter bei Vergabeverfahren, insbesondere bei Ausschreibungen von komplexen und technisch anspruchsvollen IT-Lösungen wie beispielsweise landesweite Behördennetze oder große Outsourcingvorhaben. Seit vielen Jahren untersucht er Zuschlagsformeln auf mathematische Schwächen und hat dazu unter anderem auch die UfAB Arbeitsgruppe beraten.





 (12 Bewertungen, durchschn.: 4,92aus 5)
(12 Bewertungen, durchschn.: 4,92aus 5)









Schreibe einen Kommentar