 Im letzten Faktencheck Vergabemathematik (s. Vergabeblog.de vom 22/01/2024, Nr. 55542) wurde nachgewiesen, dass man bei der Zuschlagsformel Z = L/P nicht sinnvoll von einer Gewichtung, und schon gar nicht von einer 50 %-Gewichtung sprechen kann. Aber ist es möglich, das anderweitig umzusetzen?
Im letzten Faktencheck Vergabemathematik (s. Vergabeblog.de vom 22/01/2024, Nr. 55542) wurde nachgewiesen, dass man bei der Zuschlagsformel Z = L/P nicht sinnvoll von einer Gewichtung, und schon gar nicht von einer 50 %-Gewichtung sprechen kann. Aber ist es möglich, das anderweitig umzusetzen?
Die Einfache Richtwertmethode mit Gewichtung
Sehen wir uns dazu folgende Zuschlagsformel Z(A) für ein Angebot A mit L(A) Leistungspunkten und einem Wertungspreis von P(A) mal näher an:
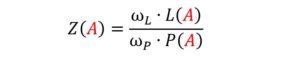
ωL stellt die „Gewichtung“ der Leistung dar, ωp diejenige des Preises. Dabei soll gelten: ωL + ωp = 1.
Beispielsweise könnte man die Leistung mit 40 % gewichten und hätte damit folgende Zuschlagsformel:
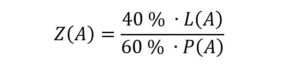
Oder man wertet den Preis mit 30 %:
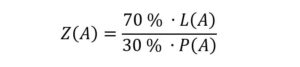
Rechnet die Formel richtig?
Nun kann man sich die Frage stellen, ob die Gewichtung bei der Berechnung von Z überhaupt korrekt berücksichtigt wird. Dazu sehen wir uns ein Angebot mit L(A) = 5.000 Punkte (analog zur UfAB, wo ein Angebot bis zu 10.000 Punkte erreichen kann) und P(A) = 10.000 Euro als Wertungspreis an. Bei einer Gewichtung von ωL = 60 % ergibt sich für dieses Angebot eine Zuschlagkennzahl Z(A) (bei einer Skalierung mit dem Faktor 10, den wir der besseren Lesbarkeit halber einfügen):
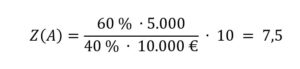
Wenn wir prüfen wollen, ob die Gewichtung bei der Berechnung von Z korrekt berücksichtigt wird, dann müssen wir mit die Leistungskennzahl nach oben und unten variieren und sehen, wie (stark) die Zuschlagkennzahl Z darauf reagiert. Sehen wir uns also mal die resultierenden Z-Werte an, wenn man L von 1.000 bis 10.000 verändert:
| 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | 10000 | |
| 60 % | 1,5 | 3,00 | 4,50 | 6,00 | 7,50 | 9,00 | 10,50 | 12,00 | 13,50 | 15,00 |
Wie man sieht, verändert sich das (skalierte) Z immer um den Wert 1,5, wenn man L um 1000 verändert. 1,5 ist aber gerade das Verhältnis von 60 % zu 40 %, also die Gewichtung der Leistung im Verhältnis zur Gewichtung des Preises. Und das ist das gewünschte Verhalten der Gewichtung.
Wir können uns das auch für andere Gewichtungen von L ansehen, siehe folgende Tabelle:
| 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | 10000 | |
| 30 % | 0,43 | 0,86 | 1,29 | 1,71 | 2,14 | 2,57 | 3,00 | 3,43 | 3,86 | 4,29 |
| 40 % | 0,67 | 1,33 | 2,00 | 2,67 | 3,33 | 4,00 | 4,67 | 5,33 | 6,00 | 6,67 |
| 50 % | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | 9,00 | 10,00 |
| 60 % | 1,5 | 3,00 | 4,50 | 6,00 | 7,50 | 9,00 | 10,50 | 12,00 | 13,50 | 15,00 |
| 70 % | 2,33 | 4,67 | 7,00 | 9,33 | 11,67 | 14,00 | 16,33 | 18,67 | 21,00 | 23,33 |
Beispielsweise ergibt sich für eine Gewichtung der Leistung von 30 % jeweils eine Steigerung um den Wert 0,43 (gerundet) je 1.000 Leistungspunkten, also genau dem Gewichtungsverhältnis 30 % zu 70 %.
Den resultierenden Steigerungswert je nach Gewichtung kann man übrigens immer bequem in der zweiten Spalte (zu L=1.000) ablesen.
Folgende Abbildung visualisiert die Rechenergebnisse der letzten Tabelle:
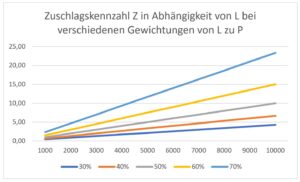
Je höher die Gewichtung von L ist, umso steiler steigt die Gerade, die die Abhängigkeit der Zuschlagkennzahl Z vom Leistungskennwert L zeigt. Die Steigung der einzelnen Geraden ist gleichzeitig das Gewichtungsverhältnis zwischen L und P.
Zwischenfazit
Die Einfache Richtwertmethode mit Gewichtung berücksichtigt für die Berechnung der Zuschlagskennzahl Z die Gewichtung der Leistung (im Verhältnis zur Gewichtung des Preises) korrekt!
Grenzen der Gewichtung
Bei vielen Schulungen frage ich die Teilnehmer, welche der folgenden Formeln besser, schlechter oder überhaupt nicht gut als Zuschlagsformel geeignet wäre:
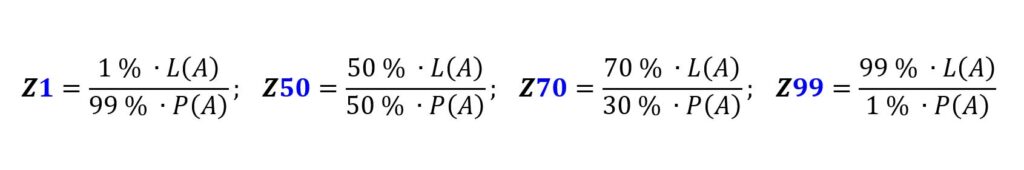
Die vier Formeln unterscheiden sich also nur im Gewichtungsverhältnis von L und P.
Im Mittel ergibt sich aus diesen Umfragen in etwa folgende (subjektive) Einschätzung der Schulungsteilnehmer:
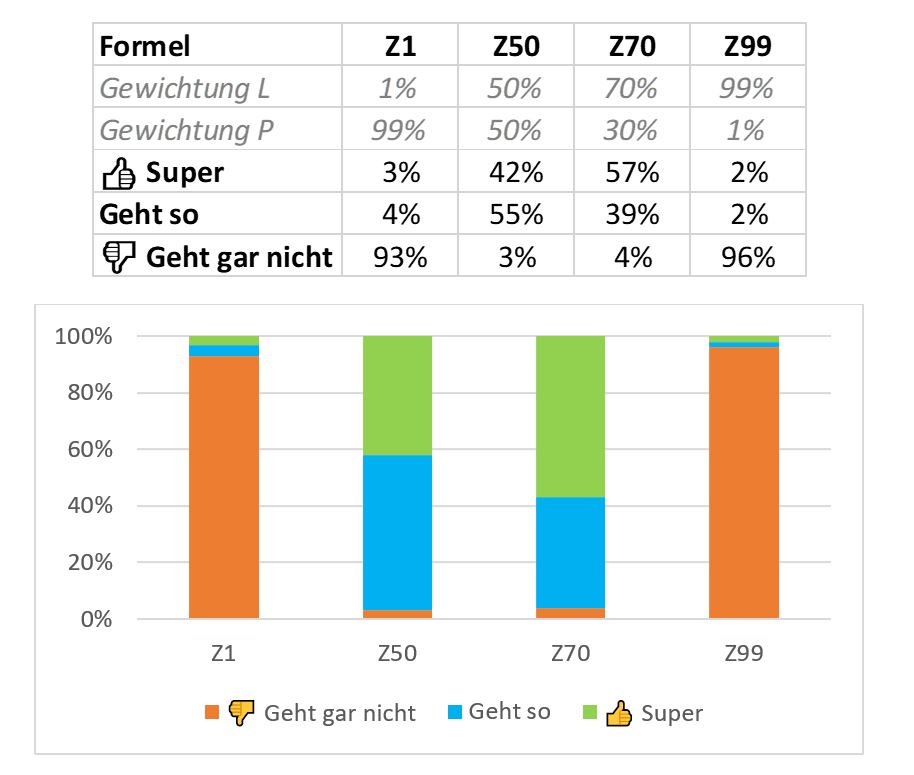
Würden Sie diese Einschätzung teilen? Die Formeln mit den extremen Gewichtungen von 1 % bzw. 99 % werden von den Schulungsteilnehmern gefühlsmäßig rundheraus abgelehnt. Die Formel mit der 70 %-Gewichtung kommt ein stückweit besser weg als die Formel mit der (expliziten) 50 %-Gewichtung (und das war schon so vor dem Erscheinen des ersten Faktencheck Vergabemathematik Artikels, Vergabeblog.de vom 22/01/2024, Nr. 55542).
Sehr viele Teilnehmer haben regelmäßig zum Teil sehr alte Beschlüsse im Hinterkopf, dass der Preis beispielsweise eine Mindestgewichtung von 30 % haben solle (OLG Dresden, Beschlüsse vom 05.01.2001 – WVerg 0011/00 und WVerg 0012/00).
Auf was kommt es am Ende an?
Ziel der obigen rechnerischen Übung ist es aber letztlich, nicht riesige Rechenwerke und Tabellen aufzustellen. Sondern eine Rangfolge der wertungsfähigen Angebote zu bilden, um das wirtschaftlichste Angebot zu identifizieren. Hilfsweise bedient man sich dazu der Berechnung einer Zuschlagskennzahl Z. Die Zuschlagskennzahl Z soll die Wirtschaftlichkeit repräsentieren; das Angebot mit der höchsten Zuschlagskennzahl erhält den Zuschlag, d. h. die Rangfolge bestimmt sich aus der Zuschlagskennzahl Z.
Sehen wir uns das mal anhand des Beispiels aus der UfAB 2018 an, welches dort einheitlich und seit mindestens 20 Jahren (seit der UfAB III) verwendet wird:
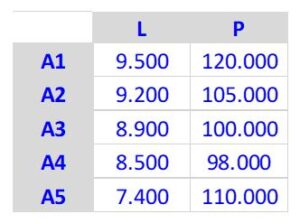
Für dieses UfAB-Beispiel berechnen wir die Rangfolgen bei verschiedenen Gewichtungsverhältnissen zwischen L und P. Die erste Zeile der folgenden Tabelle zeigt die Gewichtung von L; die Gewichtung von P ist dann die Differenz auf 100 %. Der jeweilige Zelleneintrag zeigt den Rang des jeweiligen Angebots bei der entsprechenden Gewichtung von L:
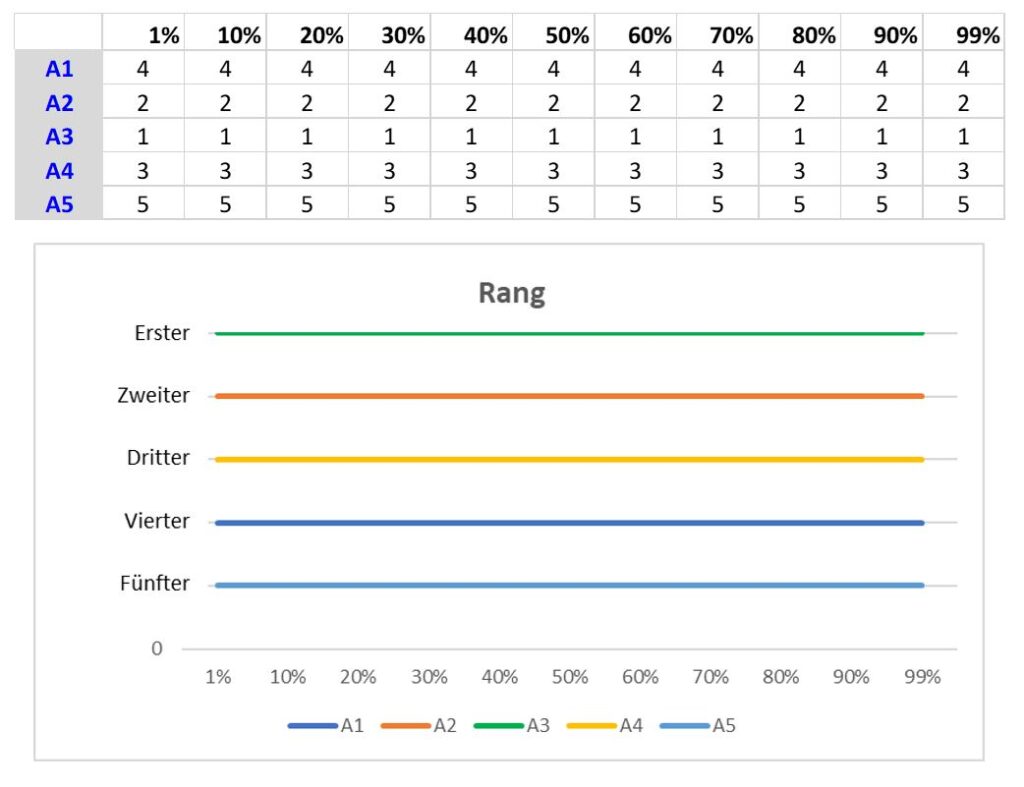
Es stellt sich heraus, dass die Gewichtung von L in diesem Beispiel überhaupt keinen Einfluss auf die Rangfolge der Angebote nimmt!
Und man kann sehr leicht mathematisch zeigen, dass dies bei der Einfachen Richtwertmethode mit Gewichtung immer so ist. Denn man kann die Formel einfach umschreiben zu:
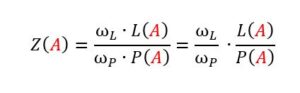
Denn dann sieht man sofort, dass ωL / ωp einfach nur eine konstante Zahl in der Zuschlagsformel ist, nämlich das Gewichtungsverhältnis von L und P. Damit ist diese konstante Zahl aber nichts anderes als eine Skalierung der Zuschlagsformel, ähnlich wie wir sie im Eingangsbeispiel dieses Artikels schon verwendet hatten (dort hatten wir mit der Zahl 10 skaliert). Diese Konstante ist für alle Angebote identisch. Daher ändert sich nichts an der Rangfolge der Angebote – egal, welche Gewichtungsfaktoren man wählt!
Beispielsweise ergibt sich aus einer Gewichtung von 60 % für L ein Gewichtungsverhältnis von 60 % zu 40 %, also 60 % / 40 % = 1,5 als konstante Zahl / Skalierungsfaktor, also die Steigerungszahl aus dem ersten Beispiel dieses Artikels.
Wirkt nicht über den Placeboeffekt hinaus
Einige Leserinnen und Leser haben bereits zu Beginn des Artikels „den Braten gerochen“, dass ich eine Formel vorgestellt habe, bei der die Gewichtung von Leistung und Preis überhaupt keinen Einfluss auf die Rangfolge der Angebote nimmt, sondern bestenfalls einen psychologischen Effekt bewirkt. Ich hatte aber dazu auch die allereinfachste und offensichtlichste Zuschlagsformel gewählt. Und wie die Umfragen in meinen Schulungen häufig zeigen, ist die Wirkungslosigkeit der Gewichtung selbst bei diesen Formeln für sehr viele Personen eben nicht so offensichtlich erkennbar.
Wenn das schon bei einer sehr einfachen Formel gar nicht mal so einfach zu erkennen ist, wie soll man dann bei komplexeren Zuschlagsformeln wie der Interpolationsmethode oder der UFAB-II Formel erkennen können, ob bzw. welchen Einfluss die dort verwendeten Gewichtungskoeffizienten auf die Rangfolge haben? Umso mehr, als die Formeln selbst bei identischen Gewichtungskoeffizienten zu verschiedenen Rangfolgen der Angebote führen können (siehe dazu das erste Beispiel aus dem letzten Faktencheck Vergabemathematik, Vergabeblog.de vom 22/01/2024, Nr. 55542). Wir verwenden dann scheingenaue Formulierungen wie z.B. „Der (Wertungs-)Preis wird mit 60 % berücksichtigt.“, ohne auch nur ansatzweise sagen zu können, wie sich ein Gewichtungskoeffizient für den Preis tatsächlich auf die Rangfolge der Angebote auswirkt. Beträgt die Auswirkung dann also wirklich 60 %? Oder nur 54,7 %. Oder gar 87,1 %. Oder vielleicht nur 2,7 %?
Durch solch eine Angabe von scheinbaren Gewichtungsverhältnissen zwischen Leistung und Preis oder Verwendung entsprechender Gewichtungskoeffizienten in Zuschlagsformeln gaukelt sich der Auftraggeber nicht nur selbst, sondern auch den Bietern falsche Tatsachen vor! Niemand ist in der Lage, eine tatsächliche Höhe der Gewichtung des Preises bei der Rangfolgebildung der Angebote zu beziffern.
Praxistipp
Trauen Sie keinen Zuschlagsformeln mit angeblicher Gewichtung zwischen Leistung und Preis, und schon gar nicht den Werten der Gewichtungskoeffizienten in solchen Formeln. Zumindest so lange Sie nicht restlos verstanden haben, wie sich diese Koeffizienten (scheinbare Gewichtungsangaben) tatsächlich auf die Rangfolge der Angebote auswirken.
Wolfgang Bartsch
Dipl.-Inform. (univ.) Wolfgang Bartsch ist Managing Consultant im Bereich Beschaffungsberatung bei der IABG mbH. Er berät öffentliche Auftraggeber und Bieter bei Vergabeverfahren, insbesondere bei Ausschreibungen von komplexen und technisch anspruchsvollen IT-Lösungen wie beispielsweise landesweite Behördennetze oder große Outsourcingvorhaben. Seit vielen Jahren untersucht er Zuschlagsformeln auf mathematische Schwächen und hat dazu unter anderem auch die UfAB Arbeitsgruppe beraten.


 (15 Bewertungen, durchschn.: 4,73aus 5)
(15 Bewertungen, durchschn.: 4,73aus 5)










Schreibe einen Kommentar