 Öffentliche Auftraggeber legen zunehmend Wert auf die Qualität der Beschaffungsgegenstände. Der Preis alleine entscheidet immer weniger. Und das ist auch gut so. Aber Qualität hat ihren Preis, und der steigt bei höchsten Qualitäten (Exzellenzniveau) häufig überproportional. Im Folgenden wird eine Zuschlagsformel vorgestellt, die sich von entsprechenden Gewichtungsproblemen unabhängig macht.
Öffentliche Auftraggeber legen zunehmend Wert auf die Qualität der Beschaffungsgegenstände. Der Preis alleine entscheidet immer weniger. Und das ist auch gut so. Aber Qualität hat ihren Preis, und der steigt bei höchsten Qualitäten (Exzellenzniveau) häufig überproportional. Im Folgenden wird eine Zuschlagsformel vorgestellt, die sich von entsprechenden Gewichtungsproblemen unabhängig macht.
Exzellenz ist übermäßig teuer
Es begegnet uns ständig: Je höher eine Leistungsqualität ist, umso teurer wird es. Ab einem gewissen Punkt der Exzellenz steigt die Teuerung aber überproportional.
Beispiel Flugpreise: Falls Sie beispielsweise heute (01.04.2024) von München nach Los Angeles fliegen wollen, dann bezahlen Sie folgende Ticketpreise (abgerufen am 09.03.2024):
| Economy | Premium | Business | Firstclass |
| 1.646,70 € | 2.422,70 € | 5.342,70 € | 12.664,32 € |
Veranschaulicht man sich die Preissteigerungen, dann erkennt man eine typische Kurvenform, die ich „Exzellenzkurve“ nennen möchte, und die uns ständig begegnet:
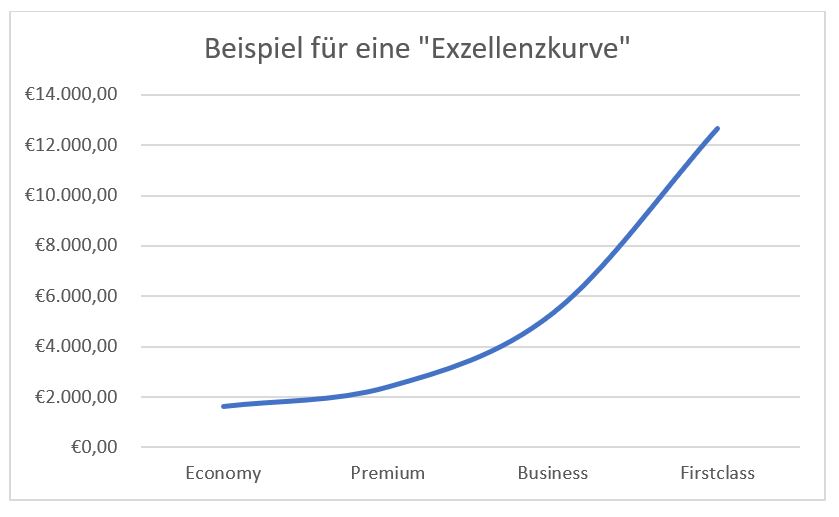
Tatsächlich ist ja die Grundleistung, nämlich dass man von München nach Los Angeles und zurück transportiert wird, zunächst identisch. Auch starten und landen alle Passagiere um exakt dieselbe Uhrzeit.
Natürlich sitzt man aber in der Firstclass wesentlich bequemer als in der Economy. Und das Essen und die Weine sind reichhaltiger und hochwertiger. Der Tomatensaft ist allerdings identisch in allen Klassen. Und die Fluglinie beteuert, dass das Flugpersonal in allen Klassen gleich freundlich und serviceorientiert sei. Die Piloten sind sowieso dieselben für alle Klassen.
Ist die Firstclass also wirklich siebenmal besser als die Economy? Das muss natürlich jeder für sich beantworten. Als Beschaffer eines öffentlichen Auftraggebers müssen wir jedoch sorgfältig mit den Steuergeldern der Bürgerinnen und Bürger umgehen.
Einerseits benötigen wir oft die höchstmögliche Qualität, aber andererseits sind die verfügbaren Mittel begrenzt.
Es stellt sich also die Frage, ob es ein „Gegenmittel“ gegen die exponentielle Kostenexplosion bei exzellenten Leistungen gibt. Denn viele Zuschlagsformeln führen heute bei der Anwendung zu oft nicht nachvollziehbaren Zuschlagsergebnissen, da Abhängigkeiten von den Preisen anderer Angebote bestehen (Stichwort: Flipping- und Decoy-Effekt, siehe Vergabeblog.de vom 23/01/2020, Nr. 43117).
Der Logarithmus ist überall
Der mathematische Gegenspieler zur Exponentialfunktion ist die Logarithmusfunktion. Bevor Sie jetzt entnervt weiterblättern, geben Sie mir einen kurzen Moment, um Ihnen dem „Bammel“ vor diesem scheinbaren Alptraum (zumindest für Einige; vgl. Weber, Christof. (2013). Grundvorstellungen zum Logarithmus – Bausteine für einen verständlichen Unterricht) aus der zehnten Schulklasse (s. ISB Staatsinstitut für Schulqualität und Bildungsforschung München – LehrplanPLUS) zu nehmen.
Denn der Logarithmus ist allgegenwärtig, und Sie nutzen ihn häufiger, als Sie denken oder bemerken.
Ist beispielweise die Rede von fünf-, sechs-, sieben- oder (beim FC Bayern:) achtstelligen Jahreseinkommen der männlichen Profifußballspieler, dann haben Sie den dezimalen Logarithmus angewendet!
Oder die Tonleiter in der Musik: Der Standard-Kammerton a‘ (eingestrichenes a), nach dem die Instrumente eines Orchesters gestimmt werden, hat eine Tonfrequenz von 440 Hertz. Steigt man die Tonleiter um eine Oktave nach oben oder unten, kommt man wieder zum a, aber diesmal mit 880 Hertz bzw. 220 Hertz. Die Tonfrequenz verdoppelt sich also pro Oktave. Man könnte auch sagen, Musik ist im weitesten Sinn eine Aneinanderreihung von binären Logarithmen auf dem Notenblatt…
Die natürliche Logarithmusformel
Internationale Mathematiker haben komplexe Untersuchungen zu mathematischen Modellen angestellt. In einem neuen Aufsatz beschäftigen sie sich dabei damit, wie der Logarithmus Preis-Asymmetrien ausgleichen könnte (L. Raman and G. Wu: Logarithm Induced Reduction of Price Asymmetries; Preprint 2024).
Darauf aufbauend schlägt der Autor nun folgende Zuschlagsformel auf Basis des natürlichen Logarithmus (logarithmus naturalis, Formelzeichen „ln“) vor:
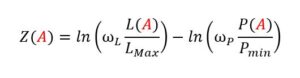
Hierbei sind:
- Z(A) die Zuschlagskennzahl für Angebot A
- L(A) und P(A) die Leistungskennzahl bzw. der Wertungspreis von Angebot A
- ωL bzw. ωP die Gewichtungen von Leistung und Preis, wobei ωL + ωp = 1
- ln der logarithmus naturalis
- LMax die maximal erreichbare Leistungskennzahl, und
- Pmin der niedrigste Preis aller wertungsfähigen Angebote
Praxistipp
Um ein Gefühl für die Anwendbarkeit der natürlichen Logarithmusformel zu erhalten, sollten Sie anhand von Beispielen die Rangfolgen der Angebote vergleichen, die sich bei der Anwendung unterschiedlicher Zuschlagsformeln wie z.B. der Logarithmusformel, der Interpolationsmethode oder der UfAB-II Formel bilden. Als Musterbeispiel eignet sich zunächst das einheitliche Beispiel aus der UfAB (cio.bund.de), aber Sie sollten auch mit überhöhten Preisen bzw. Leistungskennzahlen auf Exzellenzniveau experimentieren. Die gängigen Tabellenkalkulationen (Microsoft Excel, Libre Office Calc, …) stellen den logarithmus naturalis bereits als Funktion mit dem Namen „=LN(<Zelle>)“ zur Verfügung. Wer lieber mit dem Taschenrechner rechnet, findet zumindest auf sog. „wissenschaftlichen Taschenrechnern“ ebenfalls eine Taste „ln“. Und für Smartphones gibt es zahlreiche „wissenschaftliche Taschenrechner“-Apps, die gleichfalls den natürlichen Logarithmus implementiert haben.
Abb.: Beispiel-App für Android
Ausblick
Den Autor stört momentan noch die Verwendung von Pmin in der natürlichen Logarithmusformel. Die Verwendung von LMax ist hingegen unkritisch, da durch LMax keine Rangfolgeprobleme (Flipping-Effekt) auftreten können. Allerdings hat der Autor bei seinen Untersuchungen bereits sehr viele Szenarios mit der natürlichen Logarithmusformel durchgerechnet, und bei keinem Szenario ist der Flipping-Effekt trotz Verwendung von Pmin aufgetreten. Es sollte aber dennoch untersucht werden, ob der Formelparameter Pmin nicht beispielsweise durch den Ergebniswert der Auftragswertschätzung, die ja gemäß § 3 VgV ohnehin durchzuführen ist, ersetzt werden könnte, um den Flipping-Effekt auszuschließen.
Wolfgang Bartsch
Dipl.-Inform. (univ.) Wolfgang Bartsch ist Managing Consultant im Bereich Beschaffungsberatung bei der IABG mbH. Er berät öffentliche Auftraggeber und Bieter bei Vergabeverfahren, insbesondere bei Ausschreibungen von komplexen und technisch anspruchsvollen IT-Lösungen wie beispielsweise landesweite Behördennetze oder große Outsourcingvorhaben. Seit vielen Jahren untersucht er Zuschlagsformeln auf mathematische Schwächen und hat dazu unter anderem auch die UfAB Arbeitsgruppe beraten.


 (13 Bewertungen, durchschn.: 4,69aus 5)
(13 Bewertungen, durchschn.: 4,69aus 5)










Schreibe einen Kommentar