Die VK Bund kritisiert in ihrem Beschluss vom 03.03.2015 – VK 1-4/15, dass bestimmte Zuschlagsformeln preislich höhere Angebote im Vergleich zu anderen Zuschlagsformeln tendenziell bevorzugen bzw. weniger sanktionieren würden.

Vor diesem Hintergrund erkannte die Vergabekammer zwar objektiv einen Vergaberechtsverstoß, wies den Nachprüfungsantrag im Ergebnis aber mangels einer subjektiven Rechtsverletzung beim eher teurer anbietenden Antragsteller als unbegründet zurück, da sich die Zuschlagschancen des Antragstellers bei Anwendung anderer Zuschlagsformeln noch verschlechtert hätten – vgl. Vergabeblog.de vom 07/07/2015, Nr. 22924: „Formeltransparenz erforderlich – mit welchen Konsequenzen?“. Zu Recht?

Grund genug also, sich in folgendem interdisziplinären Vergabeblog-Exkurs der Angelegenheit mathematisch zu nähern.

Formelvarietät

Für die Umrechnung des Angebotspreises in Wertungspunkte („Preispunkte“) gibt es mehrere alternative Formeln, mit denen die Umsetzung der in den Vergabeunterlagen festgelegten Vorgaben scheinbar möglich ist. Zu nennen sind hier – als die in der Praxis am häufigsten anzutreffenden Methoden – die UfAB-II Formel, die Interpolationsmethoden sowie die Gewichteten Richtwertmethoden der UfAB (Median-, Referenzwert- und Mittelwertmethode):

– die UfAB-II Formel:

Preispunkte = 30 x P_min / P_Angebot

– die einseitige Interpolationsmethode, die zwischen dem niedrigsten und dem Doppelten des niedrigsten Preises interpoliert – einseitig deswegen, weil die Interpolation nur vom niedrigsten Angebotspreis P_min abhängt:

Preispunkte = 30 x (2 – P_Angebot / P_min)

– die beidseitige Interpolationsmethode, die zwischen dem niedrigsten und dem höchsten Preis interpoliert – beidseitig deswegen, weil die Interpolation von zwei Werten P_min und P_max abhängt:

Preispunkte = 30 x (P_max – P_Angebot ) / (P_max – P_min )

(Die Korrektheit der Formel für die Ermittlung der Preispunkte kann man leicht nachvollziehen, indem man P_Angebot = P_min einsetzt. Die einseitige Interpolation ist eine Spezialausprägung der beidseitigen Interpolation, die sich ergibt, indem man P_max = 2 x P_min einsetzt.)

Die ebenfalls mit einer Preis-Leistungsgewichtung arbeitenden Gewichteten Richtwertmethoden der UfAB (Median-, Referenzwert- und Mittelwertmethode) basieren alle auf folgender Grundform:

Sie unterscheiden sich nur in der Art der Normierung von Leistung und Preis, nämlich Normierung auf den Median bzw. auf einen vorgegebenen Referenzwert bzw. auf den Mittelwert der Leistungskennzahlen respektive der Angebotspreise der wertungsfähigen Angebote.

Visualisierung

Ohne Beschränkung der Allgemeinheit gehen wir in den folgenden Darstellungen davon aus, dass der niedrigste Angebotspreis P_min den Wert 300 betragen soll. Durch simple Skalierung können die folgenden Erläuterungen auf jeden beliebigen anderen Angebotspreis umgerechnet werden, zum Beispiel 42 Tsd. €, 2,718 Mio. US-$ oder 3,14159 Mrd. Yen.

Der Angebotspreis von 300 wird als niedrigster Preis also auf 30 Preispunkte abgebildet. Folgende Abbildung zeigt für die verschiedenen Formeln für die weiteren Angebotspreise bis 1000 die Abbildung auf die Preispunkte (30 Punkte und weniger). Als weitere Annahme wurde für die beidseitige Interpolation als höchstem Angebotspreis P_max der Wert 750 angenommen.

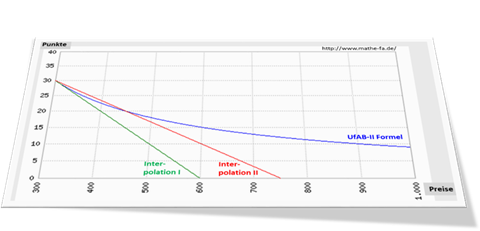
Mit der grünen Linie (in der Abbildung: Interpolation I) ist gut zu erkennen, wie für die einseitige Interpolationsmethode die Preispunktezahl gleichmäßig (linear) von 30 auf null fällt und die Null bei dem Doppelten des niedrigsten Preises P_min, also dem Abszissenwert 600 erreicht. Entsprechend fällt die beidseitige Interpolationsmethode (in der Abbildung: Interpolation II) ebenfalls linear, wenn auch unter den vorliegenden Annahmen langsamer auf 0, und schneidet die Abszisse bei dem Wert P_max = 750.

Die Kurve der UfAB-II Formel schneidet die Abszisse jedenfalls im Betrachtungsraum bis 1000 nicht – und sie wird sie auch darüber hinaus nie schneiden. Mit anderen Worten: egal wie teuer ein Angebot würde, es erhält immer noch ein paar Preispunkte aus der angewandten UfAB-II Formel. Die dritte Wertungsstufe sei für diese mathematisch-theoretische Betrachtung an dieser Stelle außen vor gelassen.

Aber kann man daraus schon schließen, dass die UfAB-II Formel teure Angebote grundsätzlich bevorzugt gegenüber anderen Zuschlagsformeln?

Vergleich der Preispunkteberechnungen

Zunächst ist erkennbar, dass die einseitige Interpolationsmethode immer unter der Kurve der UfAB-II Formel liegt, d.h. dass sie jenseits des niedrigsten Preises von 300 immer weniger Preispunkte berechnet als die UfAB-II Formel. Man kann mathematisch beweisen, dass das immer gilt, also in jedem denkbaren Szenario. Anders gesagt: Vergleicht man die einseitige Interpolationsmethode (die übrigens eine häufig empfohlene Zuschlagsformel ist und u.a. im Vergabehandbuch im Formblatt 227 fest vorgegeben ist) mit der UfAB-II Formel, so erhalten gleich teure Angebote bei Anwendung der UfAB-II Formel stets mehr Preispunkte als bei Anwendung der einseitigen Interpolationsmethode (und definitionsgemäß gleich viel Punkte – nämlich hier 30 Preispunkte – für den Wertungspreis P_min).

Die Alles-oder-Nichts Interpolation

Die beidseitige Interpolationsmethode ist da schon sperriger. Sie bildet ja das „Alles-oder-Nichts-Prinzip“ für die Preispunkteberechnung ab und ist mittlerweile berechtigterweise in die Kritik geraten (vgl. z.B. Vergabeblog.de vom 02/03/2014, Nr. 18450 oder Beschluss des OLG Düsseldorf vom 29.04.15, Verg 35/14).

Hier gilt: Liegt der höchste Preis der wertbaren Angebote P_max unter dem Doppelten des niedrigsten Preises P_min – und das sollte die weit überwiegende Regel sein –, so ist die (rote) Gerade in der vorhergehenden Abbildung noch steiler als die Gerade der einseitigen Interpolationsmethode. Und damit berechnet in diesem Fall die die beidseitige Interpolationsmethode hier stets weniger Preispunkte als die einseitige Interpolationsmethode – und erst recht weniger als die UfAB-II Formel. In diesem Fall ist also die UfAB-II Formel weniger preissensitiv als die beidseitige Interpolationsformel.

Für das niedrigste Angebot P_min berechnen alle drei Formeln natürlich den gleichen Wert, nämlich 30 Preispunkte.

Läge allerdings der höchste Angebotspreis Angebote P_max über dem Doppelten des niedrigsten Preises P_min – so wie in der Abbildung als P_max = 750 eingezeichnet–, dann berechnet die beidseitige Interpolationsmethode stets mehr Preispunkte als die einseitige Interpolationsmethode, denn die Gerade für die beidseitige Interpolation in der Abbildung liegt dann immer über der Geraden für die einseitige Interpolation – denn sie ist flacher.

Auch wenn dieses Szenario eher die Ausnahme wäre, dass der höchste Preis P_max also mehr als doppelt so hoch sei als das niedrigste Angebot aller wertungsfähigen Angebote – solche Szenarios würden regelmäßig schon in der dritten Wertungsstufe bei der Prüfung der Angemessenheit der Preise zumindest auffallen –, so ist trotzdem spannend, wie sich die beidseitige Interpolation in dieser Situation zur UfAB-II Formel verhält.

Mal so, mal so

Dazu zoomen wir mal in den Bereich kurz über dem Mindestpreis P_min hinein:

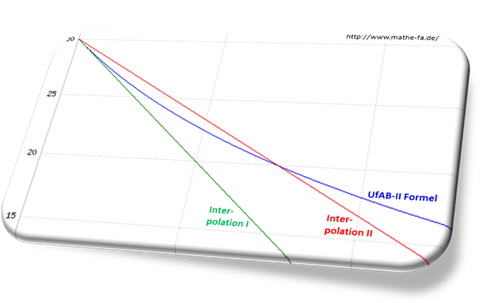
Man kann erkennen, dass die UfAB-II Formel für Preise knapp über P_min zunächst weniger Preispunkte berechnet als die beidseitige Interpolationsmethode. Erst ab dem zweiten Schnittpunkt überholt die UfAB-II Formel die beidseitige Interpolationsmethode wieder und liegt über ihr.

Und das gilt immer!

Man kann mathematisch sogar den zweiten Schnittpunkt berechnen. Denn angenommen, P_max sei das n-fache von P_min. Dann liegt der zweite Schnittpunkt bei P_min x (n-1) (beachte: n>2).

Im visualisierten Beispiel betrug ja P_max den Wert 750, also das 2,5-fache von P_min mit dem Wert 300, und damit n = 2,5. Der Schnittpunkt müsste nach der Berechnungsformel bei 300 x (n-1) = 300 x 1,5 = 450 liegen, und – voilà – da liegt er auch!

Zusammengefasst: Gerade in einiger Nähe des niedrigsten Angebotspreises P_min liefert die UfAB-II Formel weniger Preispunkte als die beidseitige Interpolationsformel, allerdings nur in dem Ausnahmefall, dass P_max mehr als das Doppelte von P_min beträgt. Anders gesagt, die beidseitige Interpolationsformel ist hier weniger preissensitiv, denn sie sanktioniert dort höhere Preise weniger als die UfAB-II Formel.

Ob eine solche Situation bei dem eingangs erwähnten Nachprüfungsverfahren vorlag, entzieht sich der Kenntnis des Autors.

Der entscheidende Faktor: Die Geradensteigung

Entscheidend dafür, ob die UfAB-II Formel also weniger Preispunkte für ein Angebot liefert als eine der linearen Interpolationsmethoden, ist die Steigung der Geraden, die die Methode visualisiert. Je flacher die Steigung, umso weniger preissensitiv ist eine Formel.

Die Steigung der einseitigen Interpolation beträgt -30 / P_min wie sich aus der Formel der Berechnung der Preispunkte ablesen lässt. Der Wert ist selbstverständlich negativ, weil die Gerade fällt und nicht steigt.

Die Steigung der beidseitigen Interpolation beträgt entsprechend -30 / (P_max – P_min ) und ist– aus genannten Gründen – ebenso negativ.

Beträgt der Wert von P_max mehr als das Doppelte von P_min, so ist der Nenner P_max – P_min größer als der Nenner bei der Steigung der einseitigen Interpolation, der ja nur P_min beträgt. Demzufolge ist die Steigung der Geraden flacher als bei der einseitigen Interpolation.

Der Nenner der Steigung entscheidet also: ist er größer als P_min, so ist die Gerade flacher als bei der einseitigen Interpolation, und die Zuschlagsformel ist zumindest in einem Bereich nahe bei P_min weniger preissensitiv als die UfAB-II Formel. Denn die Steigung der UfAB-II Formel bei P_min entspricht gerade der Steigung der einseitigen Interpolation (siehe auch unten).

Die Steigungen der Gewichteten Richtwertmethoden der UfAB

Aber ebenso wie bei den Interpolationsmethoden ist die Visualisierung der Gewichteten Richtwertmethoden eine fallende Gerade, denn der Preisterm ist linear und von folgender Form:

– 30 x P_Angebot / P_Normierung

Die drei Ausprägungen (Median-, Referenzwert- und Mittelwertmethode) der Gewichteten Richtwertmethoden unterscheiden sich nur dadurch, wie die Normierung P_Normierung gewählt wird:

– Medianmethode: P_Normierung ist der Median der Angebotspreise der wertungsfähigen Angebote (in der 4. Wertungsstufe).

– Referenzwertmethode: P_Normierung ist ein Referenzwert, den der Auftraggeber vorab in den Vergabeunterlagen bekannt gibt.

– Mittelwertmethode: P_Normierung ist der Mittelwert der Angebotspreise der wertungsfähigen Angebote (in der 4. Wertungsstufe)

Man kann leicht erkennen, dass die Geradensteigung der Gewichteten Richtwertmethoden ‑30 / P_Normierung beträgt.

Noch flacher

Nun bestimmt sich ja die die Preissensitivität einer Zuschlagsformel aus der Steigung der Geraden. Je flacher die Gerade, umso weniger preissensitiv ist die Formel.

Man kann getrost davon ausgehen, dass sowohl Mittelwert als auch Median der Angebotspreise der wertungsfähigen Angebot größer ist als der Preis des niedrigsten Angebots P_min. Das heißt, wir sind zumindest bezüglich der Median- und der Mittelwertmethode im oben beschriebenen Szenario, dass die Steigung der Geraden flacher ist als bei der UfAB-II Methode (und auch der einseitigen Interpolationsmethode). Für die Referenzwertmethode hängt dies jedoch entscheidend davon ab, wie der Referenzwert für den Preis gewählt wurde, nämlich größer oder kleiner als P_min.

Da die Steigung der Geraden ja der entscheidende Faktor für die Preissensitivität der Formel ist, kann festgehalten werden, dass die Median- und die Mittelwertmethode – sowie auch die Referenzwertmethode abhängig von der Wahl des Referenzwerts – zumindest in bestimmten Bereichen weniger preissensitiv sind als die UfAB-II Formel, d.h. dass die entsprechenden Formeln einen niedrigeren Preispunkteabschlag für eine Änderung des Angebotspreises berechnen als die UfAB-II Formel.

Zusammenfassung

Die hier vorgestellten Überlegungen zeigen, dass man nicht von der naheliegenden Annahme ausgehen kann, dass die UfAB-II Formel grundsätzlich weniger preissensitiv sei als andere Zuschlagsformeln. Zumindest theoretisch gibt es mit der beidseitigen Interpolationsmethode eine Formel, die unter Umständen in bestimmten Bereichen weniger preissensitiv ist als die UfAB-II Formel. Und weiter weisen auch die Median- und Mittelwertmethode, und – abhängig vom gewählten Referenzwert – auch die Referenzwertmethode der UfAB eine flachere Steigung auf als die UfAB-II Formel in der Nähe des niedrigsten Preises. Sie sind also zumindest in Teilbereichen ebenso weniger preissensitiv als die UfAB-II Methode.

Eine allgemeingültige Grundsatzaussage, dass die UfAB-II Formel weniger preissensitiv sei als andere übliche Zuschlagsformeln, kann insgesamt nicht getroffen werden.

Kontribution

Der Beitrag wurde gemeinsam mit Frau Dr. Reichling verfasst.

Über Dr. Ingrid Reichling

Dr. Ingrid Reichling ist Rechtsanwältin und Partnerin der Sozietät GvW Graf von Westphalen Rechtsanwälte Partnerschaft mbB. Als Leiterin der überörtlichen Praxisgruppe Vergaberecht ist sie seit 1995 auf das Vergaberecht spezialisiert und berät seitdem die öffentliche Hand ebenso wie private Unternehmen bei nationalen und europaweiten Vergabeverfahren und Ausschreibungen, Privatisierungen, PPP/ÖPP sowie bei Out-/ Insourcing. Zudem hat Dr. Reichling langjährige Erfahrung in der Vertretung bei Nachprüfungsverfahren vor den Vergabekammern und Vergabesenaten der Oberlandesgerichte ebenso sowie bei sonstigen Rechtsstreitigkeiten, Schadensersatzprozessen, bei Verhandlungen und im Vertragsmanagement. Frau Dr. Reichling ist Autorin zahlreicher nationaler und internationaler Veröffentlichungen sowie Referentin bei Fachtagungen, Seminaren und Inhouse-Schulungen zum Vergaberecht sowie Dozentin im Fachanwaltslehrgang Vergaberecht der Deutschen Anwaltsakademie.

• Profil im DVNW
|
• Alle Beiträge

Über Wolfgang Bartsch

Dipl.-Inform. (univ.) Wolfgang Bartsch ist Managing Consultant im Bereich Beschaffungsberatung bei der IABG mbH. Er berät öffentliche Auftraggeber und Bieter bei Vergabeverfahren, insbesondere bei Ausschreibungen von komplexen und technisch anspruchsvollen IT-Lösungen wie beispielsweise landesweite Behördennetze oder große Outsourcingvorhaben. Seit vielen Jahren untersucht er Zuschlagsformeln auf mathematische Schwächen und hat dazu unter anderem auch die UfAB Arbeitsgruppe beraten.

• Profil im DVNW
|
• Alle Beiträge